Home / Ultimas Noticias
Archivo Noticias de la Ciencia y la
Tecnología.
Archivo Noticias del Espacio
Contacto
Suscripciones (público/email)
Boletín Noticias de la Ciencia y la
Tecnología
Boletín Noticias del Espacio
Boletín Noticias de la Ciencia y la
Tecnología Plus
Suscripciones (servicios a
medios)
Reproducción de contenidos en medios
comerciales
|
Recuerda:
suscríbete a nuestros boletines gratuitos y recibe cómoda y
semanalmente las noticias en tu dirección electrónica.
Ciencia de los
Materiales
Cálculos Matemáticos Muestran Que Podría Existir
un Cristal Comparable al Diamante
8
de Febrero de 2008.
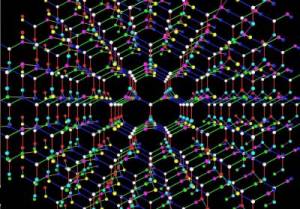 Durante
siglos, los seres humanos han quedado extasiados y cautivados por los
destellos de los diamantes. ¿A qué responde la belleza estupenda de la
gema más preciosa? Como matemático, Toshikazu Sunada explica que algunos
secretos de la belleza del diamante pueden ser desvelados por un
análisis matemático de su estructura microscópica cristalina.
 Menéame
Sucede que ésta tiene algunas propiedades muy especiales y
fundamentalmente relativas a la simetría. De hecho, como Sunada ha
descubierto, de un vasto universo de cristales matemáticos sólo otro
comparte estas propiedades con el diamante, un cristal que él denomina
el "K_4". No se sabe si el cristal K_4 existe en la naturaleza o si
podría ser sintetizado.
Se puede crear el modelo matemático idealizado de un cristal
concentrándose en sus características principales, que básicamente son
los átomos y los enlaces entre ellos. Los átomos se representan con
puntos que se denominan "vértices", y los enlaces se representan como
líneas que constituirían los "bordes". Este tipo de red de vértices y
bordes se denomina "gráfico".
El modelo matemático de un cristal se construye comenzando con el
gráfico de un bloque y uniendo luego copias de este mismo bloque de modo
periódico. Hay dos patrones que operan en un cristal: el patrón de
bordes y vértices que se unen en un bloque (es decir, el patrón de las
relaciones de vinculación entre los átomos) y el patrón periódico por el
que se unen las copias de ese bloque. De esta forma se pueden crear
incontables cristales matemáticos, variando los bloques y variando la
forma en que tales bloques se unen periódicamente.
El cristal del diamante tiene dos propiedades cruciales que lo
distinguen de otros cristales. Ninguna posible deformación del arreglo
periódico puede hacerlo más simétrico de lo que ya es. Como lo expresa
Sunada, el cristal de diamante tiene la simetría máxima.
El cristal de diamante tiene una segunda propiedad especial, denominada
"la propiedad isotrópica fuerte". Esta propiedad se parece a la simetría
rotatoria que caracteriza al círculo y a la esfera: no importa cómo se
gire un círculo o una esfera, siempre parece el mismo. El cristal de
diamante tiene una propiedad similar, que le hace parecer idéntico aún
cuando sea observado desde la dirección de bordes distintos.
Resulta que de todos los cristales que es posible construir
matemáticamente, sólo uno comparte con el diamante estas dos
propiedades. Éste es el cristal que Sunada llama K_4.
Aunque el cristal K_4 actualmente existe sólo como un objeto matemático,
es tentador preguntarse si podría existir en la naturaleza o
sintetizarse. Esto no es tan improbable como pueda parecer: el
Fullereno, con una estructura que recuerda a una pelota de fútbol, fue
identificado como un objeto matemático antes de ser encontrado
físicamente en 1990.
Información adicional en:
|
